神解是什么？在数学里，就是那些好美妙好神奇的解，恰到好处。好似飞来之笔，其实是有规律可循的。我们看一个正方形幻方的问题。
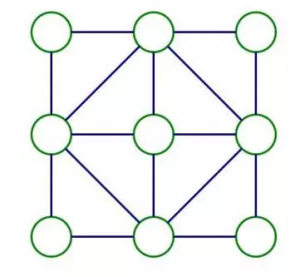
如上图所示的是一个正方形幻方。请把 1， 3， 5， 7， 9， 11， 13， 15， 17 这九个数填入到其中的圆圈中，使得每个正方形的四个角上的数字和都相等。
首先细细地审一下问题：题目要每个正方形的四角和相等，那么共有几个正方形？— 明显地是有5 个小正方形。不过您是否意识到分成小格前的大正方形也有四个角：加上它该有6 个正方形。至于考虑顺序呢：最后这条件放在最后再考查。
这题有多个常规解答，思路是列等式找规律，求解路径各有千秋。除去这些外，给大家讲一个“神”解答；奥妙全在下面的两幅图里。
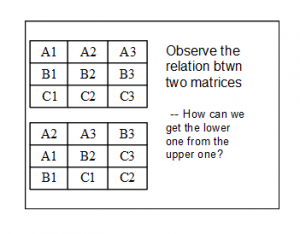
现在是见证奇迹的时刻哦，弄明白了吗？让我们把上下两个 3×3 方格分别叫做 图1 和 图2 。 图1的主对角线（A1B2C3）变成了图2里的中间一行，而图1中被对角线分开的两个拐角：右上和左下拐角，拉直后成了图2的最上和最下两行。
在图2中左上正方形的4个角点分别是 A1，A2，A3 和 B2. 他们的和不就是图1第一行和再加上B2 （中央格的数）吗？右下正方形呢？除去中央格的四个角点分别是C1，C2，C3，刚好是图1中第三行的三个数。那么如果图2中这两个正方形的四角点之和相等，等价的条件也就是图1中第一行的和，与第三行的和相等。
再注意到图二中的右上小正方形的四角和是图一中第三列数字和在加上中央格。类似地考察其他四角和条件。如每个边的中央小格连成的正方形，其数字和，要求也是同一个数。还有大正方形的四角数字和（A2 + B3 + C2 + B1）要求也是同一个数。（关于最后两条件的考察–取巧的方式是先不作 – 再说）
如果图1中的填数字是按照魔幻方要求的：即每行，每列和两个对角线的和都相等，那么图二中的数字和就已经满足了多数条件。
我们寻求一个3×3阶魔幻方由数字 1，3，5，7，9，11，13，15，17 构成。这些数可由 1，2，3，4，5，6，7，8，9 加倍（乘2）后减1得到；而按每格如此变幻后：行和，列和，对角线和仍然相等。因而由洛书图的解我们能构造一个新解（每格数字分别乘二减一），然后按前述方法把对角线和拐角拉直：对于新问题的解就来了：[他们已经满足了所有条件哦！– 包括上段所说的最后两个条件；不信你自己验证嘛] 如下面图所示。
有点神解的味道：需要对代数原理和幻方的结构非常熟悉，而巧用变换。这个漂亮的解在一次作数学模型时由参加者发现：笔者觉得其构思的巧妙不逊于 高斯在算 1+2+3+…… + 100 时所发现的规律。推荐给有兴趣的读者欣赏数学方法和构思之妙。当然，此题不必这样作，但这样的解让人觉得好美，好神！即便杀鸡不用牛刀，还是可以“牛刀小试”吧？
