高斯，全名约翰•卡尔•弗雷里奇•高斯，1777 – 1855，是德国数学家。幼时聪颖，最著名的故事就是他小学时怎样回答老师给他的那道数学题，让他算一加二加三 …… 一直加到一百。高斯从两边分别取数加起来： 1 + 100 = 101， 2+99=101，…… 如此下去刹那间就算出来结果是 50 × 101 = 5050. 这是上小学的高斯自己想出来的；稍加推广，就可以解决任何等差数列求和的问题。这是真正的天才杰作，成就了神童之誉。高斯在数学领域里终身建树颇丰，有数学王子 (Prince of Mathematics)之称。

高斯的工作涉猎数学的多个分支。除了数学外，他亦探入或与人合作探索天文和物理领域。在他的早期成长中，对于神学和语言学亦显出不同反响的理解才能。

高斯的最主要成就和他受的教育

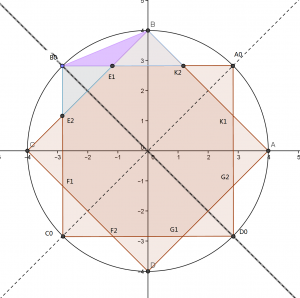
少年天才的高斯接受了正规严谨的教育，曾在卡罗琳那学院和世界知名的哥廷堡大学共学习六年（1792 – 1795, 1795 – 1798）。1796 年高斯19岁时他就发现了用直尺和圆规作正十七边形的方法：继承了来自古希腊的数学传统–只要可能的话，就只用直尺和圆规完全准确地作出任何几何图形。

1799年（22岁），高斯的博士论文改进了现在称为代数基本定理的证明。该定理说：复系数多项式至少有一个复根；通过因子分解的过程，这表明 n次多项式在复数域有n个根。在严谨性上，高斯的证明比前证明进了一大步。

高斯用直尺和圆规作正十七边形的方法，是建立在传统上的，用到了代数，还联系了可作图性与费尔马数。这成为他最得意之作；今天学习纯粹数学的人仍把它当作代数和几何结合的典范。分圆多项式理论就是在这工作中萌芽的，后得到进一步发展 （不仅是他本人的工作）。在博士论文中的证明，他自己还不满意：用了一生时间来改进代数基本定理的证明（见下文）。

非这两个工作莫属高斯一生的代表作。

其他工作

在21岁时（1798年）他完成了算术教程（这里，算术主要指现在称为‘数论’的内容 – 数论是数学中即基础又高难的一分支）。由此奠定他在数论上的地位。数论中最常用到的模同余的记号，也是由于高斯的提倡而成为标准。例如，16 除以7，余数是2，在模同余理论中，写成 16 ≡ 2 （模7）。记号≡读作同余；这大大简化了表达，体现了大家风范。

高斯还结合圆锥曲线和高次方程组（高至8次）开创了（理论）天文学的工作。其中用到了一些复杂方法如付利叶变换和三角插值。1801年（24岁），他的理论预报当年即得到天文观测的证实。此后，高斯与物理学教授Wilhelm Weber长期合作，富有成果。他建立了磁观察站和磁俱乐部，是电磁学理论的先驱之一。他的工作也涉及到光学领域。他还主持了当地大地测量（1818 年，在汉诺威王国，现为德国的一部分）。正态分布，又称误差分布，高斯分布，在实验和统计数据处理上有重要意义。高斯在其中的工作从“高斯分布”的名称上就可以看到。

我们难以尽数高斯的成就。那个 1+2+3+ … + 100 的故事，由此衍生了高斯序列（或者三角形数：如1，1+2=3，1+2+3=6，1+2+3+4=10，…； 1，3，6，10 就是三角形数）；而高斯的一个发现，是任何自然数可以写成不超过三个三角形数的和 — 来自他笔记 （”ΕΥΡΗΚΑ! num = Δ + Δ + Δ”）。喜悦之情溢于言表 — 我们看到王子在数学世界的快乐！这是1796 年，他发现正十七边形尺规作图法的同一年。这是年轻时随手的作品，是大师的小品。

他用一生的时间改进他的工作，推敲每个细节。在1849年（距首次发表已有50年之久；当时他已经72岁高龄）高斯给出了关于代数基本定理的一个证明，按近代标准完全严谨。— 天才也如此磨砺自己的工作，让人感佩！晚年高斯成为荷兰皇家协会会员及荷兰艺术科学学院院士（外籍）。他不为名所累，提携后人，欣赏同行，对新秀黎曼在曲面几何上工作由衷称赞。

高斯的启示

每个人都能够从高斯的故事和贡献中得到一些启示。少年神童很多，但是成就堪比高斯的寥寥。高斯治学毫不浮躁，终其一生改进早期已作出的成果，仅此就让今天的浮躁者汗颜。高斯既无愧于少年神童，而他的学术成就和地位却来自于追求进取和不断磨砺。为后世治学树立了榜样。