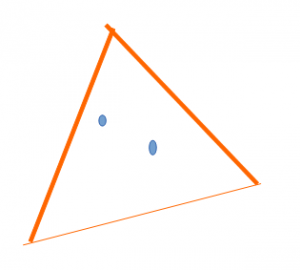
可以吗？在平面上任给５个点 (where no three points are on the same line)，可以选３个点用直线连成三角形，让另外２点都在这三角形的内部吗？有些情况下这能做到，但是总能作到吗？当这个仿佛天边飘过来的问题（既简单又似无从下手）提给 １５左右的学生时，不少就表现出跃跃欲试的兴趣。有一个立即发表意见：＂总是可以，只要找到最外面的三个点，余下的就在里面。＂

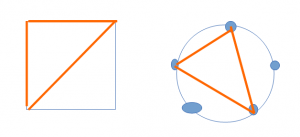
同伴反驳了，他举了一个例子：取呈正方形的四个点，无论取哪3个，都不能把另一点包含在其中。第五点呢，比方说在正方形内部。还是没办法取出含另两点在内部的三角形。
有学生补充说，如果五个点在一个圆上，都不能取出三角形把另两点含在内部喔。

教育中从简单开放的问题出发，易于参与。比方说 什么叫“最外面的点”？反驳的孩子的思路也好棒，他是举例说明有不行的情况。提醒注意，要鼓励的是探索，动脑筋思考，发表意见要重事实和逻辑，不嘲笑攻击别人。这才是安全探索的环境。和同行讨论时有共识，启发思考，东西方都有好的做法，有共通的东西。简单贴上东方,西方教育的标签，捧一个打一个，是我们一直不赞成的。

******

数学家，数学教育家 Polya 讲过（大意），好老师善于提问题引导学生深入。通过上面讨论，文章开头的问题不是总能做得到。有时能，有时不能。那么什么时候能，什么时候不能呢？可以想一下，答案在文中说明能和不能的两幅插图中找。先注重观察特征，然后再想怎么表达清楚。有兴趣的切磋一下，问问你的孩子。

问题的意义也许不在于记住答案，在于启发思考和表达。在技术和社会领域，要能够跳出框框，这也是能力。对比传统几何教育的套定理证明，这样的探索更有意义，能启发心智（传统几何自有存在意义，此另当别论）。在从众的潮流中能思考堪称可贵。

­