亲爱的读者,这是一个蛮有趣的问题:给你一个正三角形(即等边三角形),你能把它切割成几块,然后拼成一个正方形吗?
也许你完全摸不着头脑:其实这个问题是一个经典老问题。有意思的是,曾广为流传的一个解法其实是有毛病的,但却瞒过了许多人。后来才有人火眼金睛地发现了问题,经过一波三折,终于有了漂亮而完美的新解法!
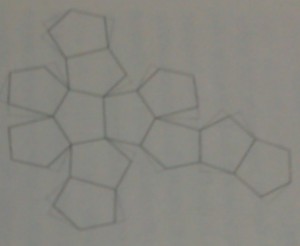
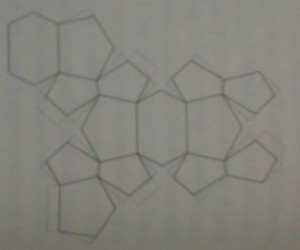
下面这张图就是曾经广为流传的一个解。(图是新画的,画的人也知道图中有误 — 但是作为数学教育,我们必须学会审视错误和偏差。)
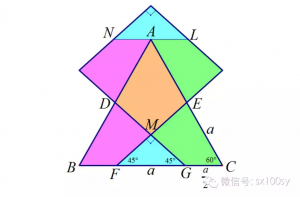 看明白了吗?参照上图:沿着ABC 的方向是一个正三角形,即AB=BC=CA (三边长相等)。把它切成四块(图中分别涂了黄绿蓝粉色),然后让绿色块以E为中心旋转180 度,粉色块以D为中心旋转 180 度,再把蓝色块移到最上端,诺,看到新成的正方形了吗?从MD,ME 分别延长出去的是两个相邻边,MA再延长到最上面的顶点是对角线。看起来活脱一个标准正方形呵,只是旋转了 45 度,对吗?从图形的对称性,新成四边形的四边都相等,应没有问题。四个角呢,那恰是环绕M的四个直角,经过翻转移动,最后变成了新四边形的四个直角。四条边相等,四个直角,那不就是正方形了吗?
看明白了吗?参照上图:沿着ABC 的方向是一个正三角形,即AB=BC=CA (三边长相等)。把它切成四块(图中分别涂了黄绿蓝粉色),然后让绿色块以E为中心旋转180 度,粉色块以D为中心旋转 180 度,再把蓝色块移到最上端,诺,看到新成的正方形了吗?从MD,ME 分别延长出去的是两个相邻边,MA再延长到最上面的顶点是对角线。看起来活脱一个标准正方形呵,只是旋转了 45 度,对吗?从图形的对称性,新成四边形的四边都相等,应没有问题。四个角呢,那恰是环绕M的四个直角,经过翻转移动,最后变成了新四边形的四个直角。四条边相等,四个直角,那不就是正方形了吗?
没有真地拿剪子裁开,拿胶水粘上去试一把,可能有些想当然了。试一试,还真能粘上。几乎大功告成之际,有人发现了破绽,看看四个角,好像不是直角哎?如果不是直角,但是四边都相等,那就只是菱形,不是正方形了。
再细看看。D,E是AB,AC 两边的中点(就是说DA=DB,EA=EC),F,G是BC的两个四分点(BF 和 GC各是BC的四分之一,FG 占了BC的一半)。(略去推导)DEGF应该是一个长方形。DG和EF呢,是这长方形的两条对角线。长方形的两对角线交成直角吗?一般不是,除非长宽相等(不信就试试)。那DE = DF 吗?DE 是正三角形边长的一半,DF呢,是三角形高的一半。高线总比边长要短些的,对不对?所以DF < DE; 于是两条对角线的交线不是直角,即环绕M的四个角都不是直角。经过翻转成为新四边形的四个角,也非直角也。
结论:新成的四边形真的不是正方形,只是菱形(也有人把它叫做钻石形–Diamond Shape)。我们计算了一下,角 FMG 大约成 98.2 度的角度。
假使没注意到交角上的破绽(不是直角),还有一个办法看出问题:既然新四边形是由原三角形裁剪拼成的,那么他们的面积应该相等咯。面积的计算稍复杂些,不再详细讨论:只提一下如果正三角形的边长是 2,那么它的面积是 3 的平方根(约为 1.73);而新四边形按照构造方法,边长应为2的平方根,所以如果是正方形,那么面积是 2,而2 不等于 3 的平方根,所以新四边形一定不是正方形!
还有操作性特强的办法发现问题:从E出发,作 DG的垂线,延长到和BC 相交。传统几何中非常讲究作图法,而且只用直尺和圆规。如果不熟悉,还是可以借助量角器完成作图,对吗?一画图就发现问题了,垂线不通过M,延长后与BC 的交点也不在F,有偏差。
能不能改正这个偏差,裁剪拼出真正的正方形呢?有的学生脑子快,马上想到一个新招。菱形是特殊的平行四边形,而平行四边形总是可以裁剪的.通过裁剪形成了四个直角。于是这位学生说,基于菱形,因为四边已经相等,所以裁剪整出四个直角后,那就是正方形了。有人反对,要裁剪两次,太麻烦了吧?而老师的意见是,麻烦不麻烦其实是第二位的,我们首先要较真一下,按这个过程得到的果真是正方形吗?
确是个好的尝试,可是有有点问题。细想一下裁剪平行四边形的过程,就发现裁剪再粘上的结果,有一边长度未变,而另一边却成了原平行四边形的高线,因而长度比原边缩短。既然裁剪前长度一样,作了这个过程后就不再相等了。当然在这问题中差别蛮小,所以得到的是长宽很接近的一个长方形。
培根有句名言:“数学使人精细。”正确求解一个可能途径是,在BC 上求一点X,使得EX刚好等于新正方形的边长。F 和 X 其实就差那么一点点。我们要做的:从原三角形的面积等于新正方形的面积,求出新正方形的边长 s,然后求F在BC上的位置, 使得 EF = s. 这是求解的第一步。正解已经呼之欲出。
说明:
1. 前辈蒋声先生最先指出开明书店旧版的 《数学万花筒》 中的一幅插图是错的,那图所指的就是化三角形为正方形的问题。真正的火眼金睛!在他后来80 年代的著作《几何变换》 中亲自改正了原图。
2. 插图取自公众号 数学教学研究,向邵勇老师致意。(他同时给出完全使用直尺圆规作图的解法。)
本文目的不在于建立严格解法,而讨论如何以审视的目光发现问题和解法的破绽。
看到和改正错误是数学的基本功之一。