分数运算的学习，涉及到两个重要方法：约分和通分。相关的两个概念，是最大公约数（GCD, or GCF – Greatest Common Factor) 和最小公倍数 (LCM – Least Common Multiple)。这两个概念是分数教学中的难点。能不能让孩子学得不那末痛苦呢？可以，我们可以引入一些数学活动或者游戏。
下面介绍在美国老师（当然是好老师）作的一个 GCF-LCM 游戏： 也可叫最简分数游戏。是一套实验教材中介绍的，下图是游戏的基本图式。给定两个数一左一右，公倍数LCM 写在上方，公约数 GCF写在下方。
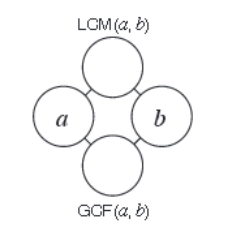
也许你说，这叫啥游戏啊？除了GCF和 LCM 的概念外，没带来新东西。也没有变化，没趣。其实不然。
我们先看求最小公倍数（LCM）的一个快捷方法：给两个数，先找GCF，然后从一个数中把GCF约去，再去乘另一个数。如求21 和 28 的LCM。找到GCF 是7，从28中约去7 得4，再用4去乘21，结果是 84. — 这就是他们的 LCM。有的学生从玩游戏中发现了这个规律。由于在图示的框架下，两个数以及GCF，LCM写在了菱形的四角上，在老师启发下学生是可以观察到规律的。在发现这个规律前，孩子通常做的是：
21 的 公倍数：21，42，63，84，105 ……
28 的 公倍数：28，56，84，112 ……圈出两个序列中相同的第一个数，就是 LCM。没有相同的，就延伸序列再找。
我们的快捷方法是不是要快得多？而且从算法上是“安全”的：如果找到的公约数不是最大的，仍然可依此算出一个公倍数，只不过不是最小的；找到的公约数太大呢？包含了不应计入的因子；那末做约分（除法）时就发现了问题：赶紧回去订正公约数。
再往前走一步，有人注意到菱形的两个对角线上的乘积相等吗？这是必需的，否则一定填写有误啦！就是说 LCM(a,b) 乘以 GCF(a,b) 的乘积一定是 ab.
稍微变一下问题。A. 如果给出两个数中的一个，再给出他们的GCF，能否求出 LCM呢？B. 给出两个数中的一个和他们的LCM，能否求出 GCF呢？
问题A可以作出好多的（无穷个）解：给出了GCF 后，我们要求另一个数要含GCF 以及不含已经在这数中的其他因子，除此以外别无限制。这样LCM有好多可能性。例如给出了一个数是21，两数的GCF是7；那末另一个数必须含因子 7，不能含因子3；但是可含因子 11，13, 或者 11 x 49，都是允许的。满足条件的一个解可能是 7 x 11 x 49: 这样的解就太多了。
问题B一般也会有多解：但是解的个数有限。因为给出了LCM，就限制了两个数都不能太大（起码不能比所给的 LCM 更大吧）。如给出一个数是28，两数的LCM是84. 注意到84 = 28 x 3, 这个3 不是28 的因子；所以一定要出现在另一个数中。这个数的其他因子一定要来自28 的因子；如 2，4，7，14 还有28. 所有可能的解是 3，6，12，21，42 和84. 这些数和 28 的LCM 是84. 至于GCF呢，就分别情况来求吧。
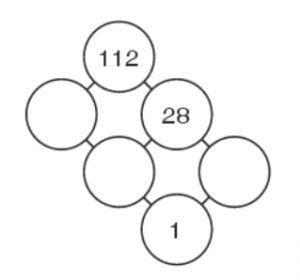看一下GCF – LCM 网。游戏变得更有趣一些了！[这类游戏编写的一个拿手好戏，就是通过组合创造一些复杂性，增加一些建立在简单基础上的挑战；增加的一点波澜，会刺激孩子的兴趣，及学会观察思考，学会自己思考解决问题。]
如图所示，要在三个圈里填数：按照基本图示理解：两数的GCF 是1， LCM 是 28. 数28 和 第三数的LCM 是 112，二者的GCF 是刚才提到的两数之一。注意至少给出一个LCM 是很重要的，否则有无穷解 （无法定解）。上例是最简单的 GCF – LCM 网，通过更多的链接，可以造出更复杂的网（也别太复杂，适可而止）。
从教育角度说两句。为啥不直接使用分数计算作题海训练呢？一是引入变化增加了趣味性，让孩子爱做配合训练；二是通过图示框架观察找规律，孩子在启发下自己发现规律才印象深，也学会思考；第三：图上作业和单用数字文字比，更有意思，也在反复中比较 GCF 和 LCM 的区别和联系；达到概念清晰，熟练基本技巧–- 其实掌握任何技巧都需要一定量的训练。学习和训练中有阈值原理，要达到定量超越阈值，学习成果才能巩固下来。说明一点: LCM 和 GCF 的概念需要在游戏前介绍 — 最好配有例子； 这个游戏不是用来讲概念的，也是为了复习概念，再熟悉计算提高运算技巧。
最后同样重要的一点，研究思维科学的人特别强调简单图示的意义：在概念形成阶段，图示能在框架下简单清晰地表达概念联系，让我们的思维聚焦。等到完全想好后再用文字写清楚。这个原理在游戏中得到了应用。 游戏作玩后告诉学生GCF，LCM 的直接应用是分数计算：这时作分数计算（通分约分）就不畏难了，还觉得兴趣盎然。[还有的老师是先教了通分约分再来介绍这个游戏 — 这样学生们可以通过游戏熟悉 GCF，LCM 的概念和计算。] 学生们对于概念的理解更加深入，计算能力也有提高 — 算得更快！
留给读者一个问题。
您能完成左边的问题吗？还有前面给出的 GCF-LCM 网的那个问题？
左边问题的解释是（回忆基本图示）：求一个数，与 22 的最小公约数是242；并且求出其与22 的最大公约数。提示：答案不唯一。
回答一下贴出后收到的问题。
有读者问，这个方法与我们学习时的完全不同。是不是人文增加了问题的复杂度？如果作分数加法，（1/2） + （2/3）， 直接就看出最小公倍数 （LCM） 是6，岂不简单得多？
回答： 这个游戏是帮助理解LCM与GCF的关系的。 对于简单运算情形，可以先教。
但是，在北美长大的孩子普遍运算能力较弱（对不起，我讲的是实话），原因不在于孩子的智力达不到，而在于教的方法，以及在这里的文化下，孩子不愿意作大量的练习 — 除非练习过程本身让他们觉得有趣。
对于稍大数的通分，这里介绍先求公约数从其中一个数中约去，再去乘另一个数的做法，确实要快一些。找公约数也比找公倍数要容易。先通过游戏训练这个方法，让孩子觉得是在玩： 两个孩子比一比，谁能把游戏里的圆圈圈最先填完 — 孩子们觉得是挺酷的； 如果做的慢一点，也不用太伤心，不过是游戏嘛。在这样一个相对轻松同时又有挑战的环境中，学习效果能达到极大化。