爱玩耍爱游戏是儿童的天性。玩游戏也可以学数学吗？当然，在一定条件下是可以的。关键是玩法得当，在高手引导下或好老师指导下收获最大，进步也快。
玩游戏学数学，非自今日提出，但是多数家长对之有戒心，可说是没成气候。究其原因呢，许多人头脑里有个框，认为学数理化就得正襟危坐，一本正经，学和玩扯不到一块。这种观念的效果不一定是促进学习，反而让孩子提不起劲学习，也给家长拿来“我的孩子不是学数学的料”，最终放松乃至完全放弃数学学习。
游戏呢不光是计算机上的数学游戏（大家对于计算机游戏已了解较多），更主要的是含有“数学元素”。
什么是数学元素呢？不只是传统的代数几何三角分析，也有逻辑，组合问题和博弈策略。这类游戏中，有的是用数学方法分析传统的游戏，让学习者看到游戏背后的数学道理（一些教师，科普期刊，网上学习站做了努力）。还有的是把数学观念或者事实融合在游戏中；在玩游戏的过程中同时应用数学概念发展游戏策略。这后一种游戏引起了教育者越来越多的认真的兴趣。这种数学游戏也可以看作是头脑实验的雏形，或者融入了数学原理的益智活动。游戏可以在计算机上玩，但是在纸上作最好。我们借这个机会分享一下。
** **
为不致空泛，我们来看两个简单游戏：1. 数独游戏； 2. 余数井跳跃游戏。涉及到的知识主要是逻辑和简单算术，尤其适合在小学高年级到刚进初中阶段（4-7 年级）的学习。
第一个是数独游戏 (Sudoku)。这个游戏的发明人就叫 Sudoku。常见的格式是一个正方形分成 3 × 3 的 9 个小正方形，每个小正方形又有 3 × 3 的9个小格子；总共81 个小格子。在每一行，每一列，每个小正方形中数字 1 – 9 都要出现一次。（中文把这个游戏译成数独，很妙！）游戏开始时在若干格子里给了数字，参加游戏的人接下去把它填好。如果给的数字少，最终填数的答案是唯一的（或有两三个也可以），那末游戏的难度就大。这个游戏吸引了很多人，很益智力，也帮助理解数学方法。
余数井游戏（Jump Between Wells of Remainders） – 示例
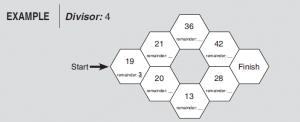第二是余数井游戏。在一张图上玩：有出发点（Start）和终点（Finish）。图的每个节点往下走常会有几条不同路径。这图比线性链条稍复杂一点，乍一看像项目管理的节点图。每节点有一个整数，出发点的上方指定了一个除数（整数）。玩法很简单，规则定步数，你选路径。每次移的步数怎末定？每到一个节点用这个节点的数除以指定的整数，商是整数（余数是0），就不能移动；不能整除就用带余除法求余，余数是几就移几步（可选不同路径），超过一步就是跳跃。从出发点开始，反复用规则。还有，只许往终点方向走，不许往回。在找到达终点的路径后游戏结束。这帮助练习带余除法，探究整除规律；也可以想出 Smart Strategy，有 Strategy 助力，更快地做完。数学知识已融入了规则，玩中也学到了。
有孩子（愿意动脑筋，理解能力较强的孩子）在规律或者Smart Strategy被揭示出来后，一下子觉得简单了。这让他们体会到数学的威力！下一步呢？我们可以让他们出游戏题给别的孩子玩。啊哈！这是新挑战。比方说余数井游戏，到达终点的路径怎样掩藏起来不易被发现？若孩子真是出了难度较大的题目，那么（如条件允许）老师可以陪孩子玩。孩子化了心思的杰作一定要多与鼓励。让孩子在兴趣盎然中动了脑筋，开始用数学工具思考，表达和发展解决问题的能力。（还有一些图形简单变换的游戏，对于孩子理解形状，提高空间想象力特别有帮助，为省篇幅从略。）
** **
知道数独游戏的人比较多；知道余数井的人少多了。您想了解更多吗？或想了解一下游戏的难点，挑战之处在哪里？我们会在以后通过具体实际例子作更详细的介绍。
请您多多关注。
谈到游戏，想作个声明。没有说学数学不要下功夫，只是玩玩就可以了。但是，在今天，社会日益多元化，日渐丰富的计算机游戏抓住了孩子们。让不同禀赋的孩子都有兴趣学数学，愿意配合学，主动学，多走一步去探究深想一下问题，如何能做到？就成为很重要的课题。兴趣与热爱是学习中不衰的动力；教育中有重新认识游戏方法的必要。想让孩子参加数学竞赛的家长：在小学阶段，不能纯逼孩子做题，要让孩子乐学；大家有兴趣研究一下竞赛题的方向，会发现很多游戏化的数学问题。真兴趣培养起来了，能力和乐于探索挑战的精神也是可以加上的。当然，游戏方法需要和其他配合，如讲清概念，专题训练，给孩子提示重点等。
只要引导得当，孩子在高中以后数学方面的兴趣充分发展了，而由于学习任务加重，系统化学习会更好。从以游戏和活动为主（小学到刚进初中）到更加系统化的学习，作为家长和老师，就是帮孩子保持了好奇心和探索的热情，并且把学习推进到了一个更高阶段。
